1. Giới thiệu
Cách chúng ta gán xác suất cho tất cả các sự kiện có thể xảy ra của một biến ngẫu nhiên phụ thuộc vào việc biến ngẫu nhiên là rời rạc hay liên tục. Sự khác biệt này rất quan trọng vì nó sẽ ảnh hưởng đến việc lựa chọn một mô hình thống kê cơ bản cho dữ liệu.
Một biến ngẫu nhiên rời rạc là một loại biến, trong đó tất cả các giá trị có thể có của biến ngẫu nhiên nhận một giá trị có thể đếm được, ví dụ: số học sinh nữ trong một lớp, số học sinh vượt qua kì thi của một trường. Sẽ không có ý nghĩa nếu đếm nửa người, hoặc một số thập phân của số học sinh vượt qua kỳ thi của một trường.
Sự phân biệt giữa rời rạc và liên tục không phải lúc nào cũng rõ ràng trong thực tế. Ví dụ, một người có chỉ số IQ trung bình có thể có số điểm khoảng 100 hoặc 101 nhưng không phải ‘101.5’. Do vậy, IQ rời rạc theo nghĩa phân loại mức độ của thang đo lường. Tuy nhiên, bản chất IQ hầu như luôn được coi là một đo lường liên tục. Lý do là bởi vì chỉ số IQ được cho là để đo lường một chiều liên tục về mặt lý thuyết của trí thông minh.
Phân phối xác suất của một biến ngẫu nhiên rời rạc có một xác suất gắn với mỗi và mọi kết quả có thể xảy ra. Nếu chúng ta vẽ biểu đồ phân phối xác suất cho một biến ngẫu nhiên rời rạc, nó tương tự như biểu đồ thanh (bar chart) tần suất tương đối, với mỗi thanh có chiều rộng đơn vị và chiều cao của các thanh biểu thị xác suất kết quả cho biến ngẫu nhiên rời rạc. Chỉ khác biệt là chúng ta thay thế tần suất tương đối của một kết quả bằng một giá trị xác suất.
2. Phân phối xác suất rời rạc
2.1. Phân phối xác suất nhị thức
Phân phối xác suất nhị thức là một dạng phân phối rời rạc thường dùng trong thống kê. Phân phối xác suất nhị thức chỉ tính đến hai trường hợp, thường được thể hiện là 1 (thành công) hoặc 0 (thất bại) trong mỗi lần thử. Phân phối xác suất nhị thức thể hiện xác suất để x lần thành công trong n phép thử, với xác suất thành công p của mỗi phép thử.
Giá trị ước lượng hoặc giá trị trung bình của một phân phối nhị thức được tính bằng cách nhân số lần thử ‘n‘ với xác suất thành công ‘p‘. Ví dụ, giá trị ước lượng của số lần tung đồng xu ra mặt ngửa trong 100 lần thử là 50, hay 100 × 0.5. Một ví dụ khác, ước tính số lần ném bóng thành công trong bóng rổ với giá trị 1 là vào rổ và giá trị 0 là ném ra ngoài.
- Giá trị trung bình của phân phối xác suất nhị thức: np.
- Phương sai của phân phối nhị thức: np(1-p).
- Độ lệch chuẩn của phân phối nhị thức tính bằng căn bậc hai của phương sai.
- Với p = 0.5; phân phối sẽ cân đối quanh giá trị trung bình.
- Khi p > 0.5; phân phối sẽ lệch về bên trái.
- Và khi p < 0.5 phân phối sẽ lệch về bên phải.
Phân phối xác suất nhị thức (P) được tính bằng cách nhân xác suất thành công p lũy thừa số lần thành công k với xác suất thất bại (1-p) lũy thừa số lần thất bại (n-k). Sau đó, nhân với tổ hợp giữa số lần thử và số lần thành công vì số lần thành công có thể được phân bố bất kì trong số lần thử. Sau đó, nhân với hệ số nhị thức, đề cập đến k thành công trong n lần thử nghiệm (sự kiện).

Ví dụ, trong nghiên cứu giáo dục, nếu chúng ta chọn một mẫu ngẫu nhiên đơn giản gồm 10 trường từ tổng thể tất cả các trường phổ thông tại một tỉnh và cho mỗi trường, chúng ta đã xếp nó vào loại ‘tốt hơn’ hoặc ‘kém hơn’, tùy thuộc vào câu trả lời cho câu hỏi sau: ‘ Tỷ lệ học sinh vào đại học là ‘tốt hơn’ hoặc ‘kém hơn’ so với tỷ lệ đậu trung bình của quốc gia (dân số) là 39.9%? ‘Chúng ta thu được số liệu từ 10 trường có tỷ lệ đậu phần trăm như sau: (với + hoặc – cho biết liệu nó tốt hơn hay kém hơn mức trung bình quốc gia): 19 (-); 37 (-); 52 (+); 11 (-); 13 (-); 31 (-); 100 (+); 25 (-); 41 (+); 18 (-).
Nếu chúng ta coi một trường được lấy mẫu nằm trên trung vị (39.9%) là thành công thì một mô hình thống kê thích hợp để mô tả phân phối xác suất của biến ngẫu nhiên (trường = thành công / thất bại) là phân phối xác suất nhị thức, đôi khi được gọi là mô hình nhị thức (Binomial Model). Phân phối xác suất này cho phép xác định xác suất cho bất kỳ số trường thành công k, (k = 0, 1, 2… 10), trong n = 10 trường học, miễn là chúng được chọn ngẫu nhiên.
Chúng ta có thể sử dụng phân phối mẫu nhị thức để trả lời các câu hỏi: “Có thể xảy ra một cách tình cờ mà chúng ta có được 3 trường trong mẫu có tỷ lệ đậu trung bình trên quốc gia không?”
Chúng ta hãy xem xét việc chọn một trường ngẫu nhiên. Điều này tương đương với một lần lật đồng xu. Xác suất trường được chọn nằm dưới mức trung bình quốc gia là bao nhiêu? Hãy nghĩ về xác suất thu được một ‘mặt ngửa’ với một lần lật đồng xu. Trong cả hai trường hợp, câu trả lời là một nửa (50%).
Bằng trực giác, có thể dễ dàng trả lời câu hỏi về cách lật đồng xu. Giả sử đồng xu là công bằng thì thậm chí có khả năng những ‘mặt ngửa’ sẽ quay lên. Lý do tại sao xác suất trường được chọn nằm dưới mức trung bình là 50% là vì theo định nghĩa một nửa dân số nằm dưới mức trung bình. Hãy nghĩ về nó theo cách này, chỉ có thể có hai kết quả, trường được chọn thấp hơn hoặc cao hơn mức trung bình dân số (hiện tại chúng ta đang giả định rằng không trường nào trong số các trường được lấy mẫu có tỷ lệ đậu bằng trung bình dân số). Do vậy, xác suất thành công ở đây là p = 0.5.
Bây giờ chúng ta có thể đánh giá xác suất nhị thức (P) bằng công thức trên:

Chúng ta có thể nói rằng xác suất chọn ngẫu nhiên 7 trường trong số 10 trường dưới mức trung bình quốc gia là 0.117 (hoặc khoảng 12%).
Điều này cho thấy rằng nếu chúng ta chọn một mẫu ngẫu nhiên thì chúng ta sẽ tình cờ mong đợi, cứ 100 trường thì có 12 trường nằm trên mức trung bình quốc gia. Câu hỏi đặt ra bây giờ, “Mức xác suất quan trọng dưới đây mà chúng ta không thể chấp nhận
rằng các kết quả được mong đợi chỉ tình cờ phát sinh là bao nhiêu?”
Điều này đưa chúng ta đến vấn đề ý nghĩa thống kê và giá trị P. Quy ước được chấp nhận chung rằng nếu chúng ta thu được xác suất nhỏ hơn ‘0.05’, được viết là P <0.05 (< nghĩa là nhỏ hơn), thì kết quả được coi là có ý nghĩa thống kê và không để phát sinh một cách tình cờ.
Vì xác suất quan sát P = 0.117 > 0.05 nên chúng ta kết luận rằng các dữ liệu này đại diện cho một mẫu ngẫu nhiên của các trường là hợp lý.
Bằng cách tính toán tương tự, chúng ta sẽ tính toán được phân phối xác xuất cho một mẫu nhị thức của n=10 và =0.5, với A là trên và B là dưới.
Phân phối 10A 9A1B 8A2B 7A3B 6A4B 5A5B 4A6B 3A7B 2A8B 1A9B 10B n trên median 10 9 8 7 6 5 4 3 2 1 0 P 033 439 0000 .044 033 439 0000 .246 033 439 0000 .044 033 439 0000
Nếu chúng ta đã quan sát thấy 8 trường trở lên trên mức trung bình, hoặc 8 trường trở lên dưới mức trung bình, chúng ta sẽ kết luận rằng rất khó có khả năng tình cờ có được loại phân phối này. Khi đó chúng ta có thể nói rằng các trường học không đại diện cho một mẫu trường học ngẫu nhiên từ tổng thể dân số.
Khi nào chúng ta sử dụng phân phối nhị thức trong nghiên cứu tâm lí và giáo dục: Bất kỳ dữ liệu nào rời rạc và có thể được mã hóa thành giá trị ‘0’ hoặc ‘1’ tương ứng với ‘thành công’ hay ‘thất bại’, tuân theo phân phối nhị thức với điều kiện xác suất cơ bản của thành công, ‘p‘, không thay đổi theo số lần thử nghiệm n. Biết phân phối cơ bản của một biến rời rạc có nghĩa là chúng ta có thể ước lượng giá trị và kiểm tra giả thuyết. Dữ liệu dưới dạng tần số, tỉ trọng hoặc tỷ lệ phần trăm rất phổ biến trong nghiên cứu tâm lí và giáo dục, và sự biến thiên của các thống kê mẫu này rất quan trọng trong việc ước lượng và suy luận. Thông thường, các loại câu hỏi mà nhà nghiên cứu có thể muốn trả lời bao gồm:
– “Chúng ta có thể có bao nhiêu sự tin cậy rằng tần suất hoặc tỉ trọng mẫu đại diện cho tỉ trọng thực tế trong dân số quan tâm?”
– “Kết quả của sự quan tâm, chẳng hạn như số người thành công, tỷ lệ vượt qua kì thi khác với những gì chúng ta mong đợi một cách tình cờ không?”
– “Tỉ trọng nam và nữ trốn học trong trường có giống nhau không?”
Trường hợp 1: Ứng dụng của trung bình và độ lệch chuẩn của biến nhị thức
Xác suất để một trường trung học cơ sở có tỷ lệ học sinh vắng mặt trái phép > 1% là P = 0.5. Điều này được tiên nghiệm dựa trên số liệu của Bộ Giáo dục và Đào tạo cho năm trước. Nếu chúng ta dự định chọn một mẫu ngẫu nhiên đơn giản gồm 500 trường trung học cơ sở, giá trị trung bình và độ lệch chuẩn dự kiến của số trường có tỷ lệ vắng mặt trái phép > 1% là bao nhiêu?
Sử dụng mô hình xác suất nhị thức, mỗi trường có xác suất cơ bản là 0.5. Số trường trung bình bằng:
Mean = np = (500) × (0.5) = 250
Như vậy, chúng ta hy vọng sẽ tìm thấy 250 trường trong mẫu có tỷ lệ học sinh vắng mặt trái phép > 1% và có độ lệch chuẩn sẽ là:
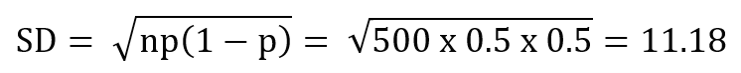
Trường hợp 2: Ứng dụng của tỉ lệ mẫu (hoặc phần trăm mẫu)
Tỉ lệ mẫu hoặc phần trăm mẫu là những giá trị phổ biến trong nghiên cứu tâm lý và giáo dục, và phân phối mẫu của thống kê đó cho phép các nhà nghiên cứu làm các suy luận thống kê về các tỉ lệ (hoặc phần trăm) trong dân số.
Ví dụ, một nghiên cứu báo cáo rằng 30% sinh viên không thể hoàn thành đầy đủ bài thi Toán giải tích. Nếu một mẫu 60 sinh viên là một mẫu ngẫu nhiên đơn giản, thì trung bình, chúng ta kì vọng 30% dân số (P=18/60=0.3) không thể hoàn thành nhiệm vụ.
Chúng ta tự tin đến mức nào với độ chính xác thực tế của ước lượng này? Để trả lời câu hỏi này, chúng ta chuyển sang xem xét các sai số chuẩn và khoảng tin cậy.
2.2. Sai số chuẩn
Độ lệch chuẩn của một phân phối mẫu của một thống kê là sai số chuẩn của thống kê đó. Các nhà thống kê sử dụng các sai số chuẩn để xây dựng khoảng tin cậy từ dữ liệu mẫu của họ. Khoảng tin cậy rất quan trọng để xác định tính hợp lệ của các bài kiểm tra thống kê. Ví dụ, khoảng tin cậy thông thường cho chúng ta biết rằng có 95% khả năng chúng ta bỏ lỡ trung bình dân số thực bằng cách cộng hoặc trừ hai sai số chuẩn.
Sai số chuẩn đôi khi bị nhầm lẫn với độ lệch tiêu chuẩn. Sai số chuẩn thực sự đề cập đến độ lệch chuẩn của các giá trị trung bình của các phân phối mẫu. Độ lệch chuẩn (standard deviation) đề cập đến sự thay đổi bên trong bất kỳ một mẫu nào, trong khi sai số chuẩn là sự biến thiên của các phân phối mẫu. Độ lệch chuẩn mô tả sự lan truyền của các giá trị trong một mẫu, nhưng nó vẫn giữ nguyên trung bình khi kích thước mẫu tăng hoặc giảm. Sai số chuẩn là độ lệch chuẩn của giá trị trung bình mẫu và mô tả độ chính xác như là ước tính của trung bình dân số. Khi kích thước mẫu tăng, công cụ ước tính dựa trên nhiều thông tin hơn và trở nên chính xác hơn do đó khả năng xảy ra sai số chuẩn giảm và ngược lại.
Khi chúng ta lấy một mẫu, chúng ta thường ước lượng một số tham số như giá trị trung bình và độ lệch chuẩn. Sai số chuẩn là thước đo của một loại sai số trung bình mà chúng ta có khả năng mắc phải trong ước tính của chúng ta. Hãy tưởng tượng chúng ta lấy tất cả các mẫu có thể, và từ mỗi mẫu chúng ta tính toán ước tính của chúng ta. Điều này tạo ra một quần thể ước tính mới. Độ lệch chuẩn của dân số này là sai số chuẩn. Tuy nhiên, việc lấy tất cả các mẫu có thể là không thực tế, nhưng lý thuyết thống kê thường cho phép chúng ta tính ra sai số chuẩn hoặc ước tính nó từ một mẫu duy nhất.
Sai số chuẩn đượ ước tính là: 
Trong đó P là tỷ lệ quan tâm của mẫu và n là cỡ mẫu.
Ví dụ, sai số chuẩn của tỷ lệ mẫu sinh viên không thể hoàn thành đầy đủ chính xác bài thi môn Toán giải tích là:

Sai số chuẩn là một chỉ số về sự chính xác, là một chỉ báo về số sai số của kết quả khi một thống kê mẫu đơn lẻ, ở đây là một tỷ lệ, được sử dụng để ước tính tham số dân số tương ứng.
Sai số chuẩn càng lớn thì ước tính càng kém chính xác. Sai số ch
uẩn liên quan đến cả kích thước mẫu và tính không đồng nhất trong dân số. Kích thước mẫu lớn hơn làm giảm sai số chuẩn vì chúng ta chia cho một mẫu số lớn hơn. Sự không đồng nhất lớn hơn trong dân số, tức là một phương sai lớn hơn, làm tăng sai số chuẩn. Trong ví dụ này, khi tỷ lệ thành công tiến gần đến 0.5, tử số tăng lên, do đó làm tăng kích thước của sai số chuẩn. Khi tổng thể trở nên đồng nhất hơn, tức là P có xu hướng về 0 hoặc 1, thì độ biến thiên mẫu sẽ giảm. Khi lập kế hoạch nghiên cứu, cần xem xét cả cỡ mẫu và phương sai của các biến quan trọng.
Thường có sự nhầm lẫn về việc liệu nên báo cáo độ lệch chuẩn hay sai số chuẩn trong báo cáo khoa học. Độ lệch chuẩn mẫu (sample standard deviation) là thước đo sự trải rộng của các điểm số thô và do đó cần được báo cáo, với giá trị trung bình, khi mục đích là mô tả phân phối dữ liệu. Sai số chuẩn là một chỉ số về độ chính xác của một thông số ước tính và cần được báo cáo khi mục đích là so sánh các ước lượng thông số, ví dụ, khi so sánh các trung bình cho các hiệu quả điều trị khác nhau. Chúng ta nên đặt các thanh sai số chuẩn chứ không phải các thanh độ lệch chuẩn trên một biểu đồ để so sánh các giá trị trung bình điều trị.